Technology for Humanity

Prediction of the 10-year Cardiovascular Heart Disease Using the Framingham Heart Study Data

Chapter 3. Data Clean-Up

Once confirming the integrity of data (see Chapter 2), clean-up the data for analysis. First, visulization.

Step 1: Selection of features (i.e., variables)

# checking distributions using histograms


fig = plt.figure(figsize = (15,20))
ax = fig.gca()
df.hist(ax = ax)

Figure 1. Histograms of all variables

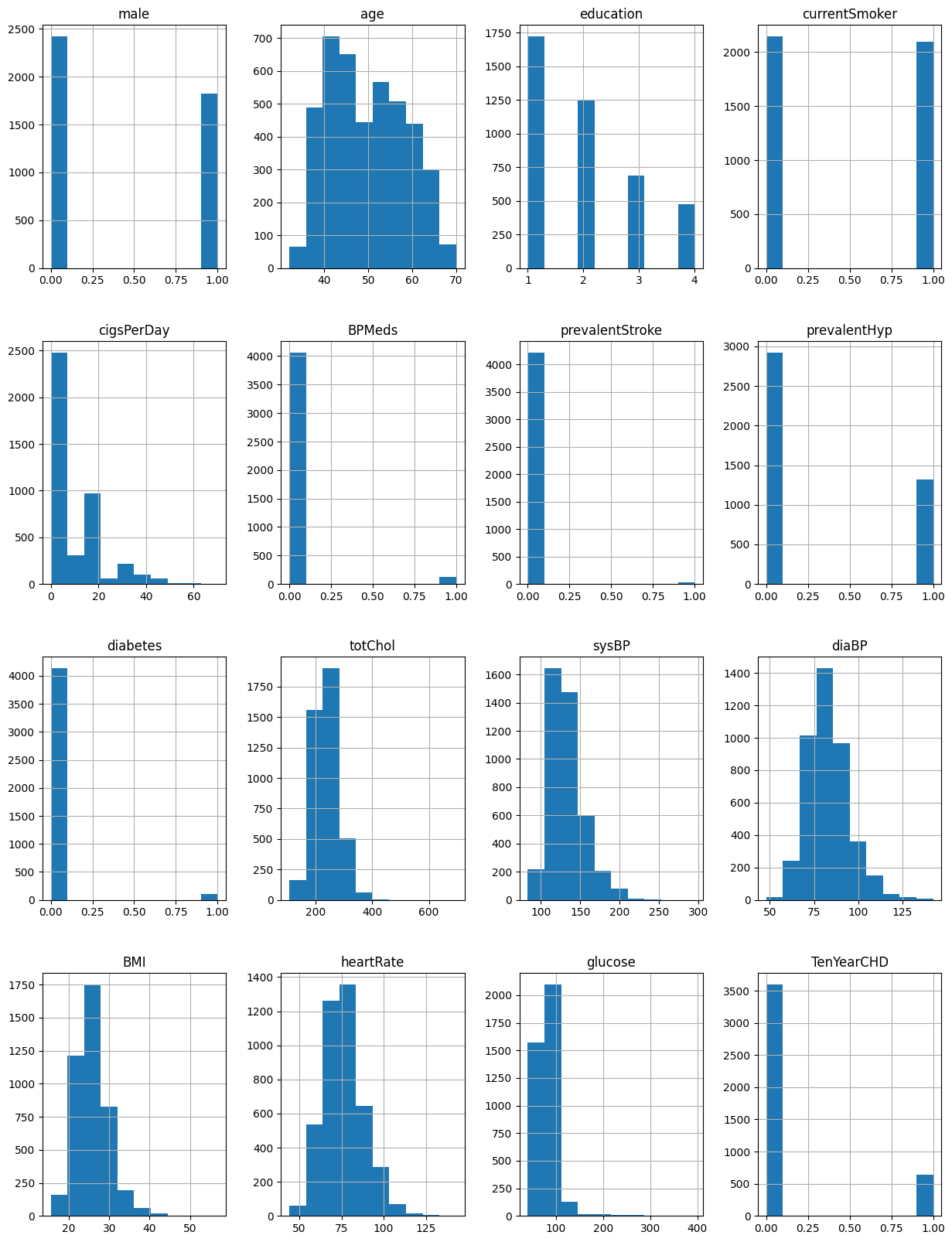
# checking which features are correlated with each other and are correlated with the outcome variable.


df_corr = df.corr()
sns.heatmap(df_corr)
plt.show()

Figure 2. Heatmap - visual representation of correlation

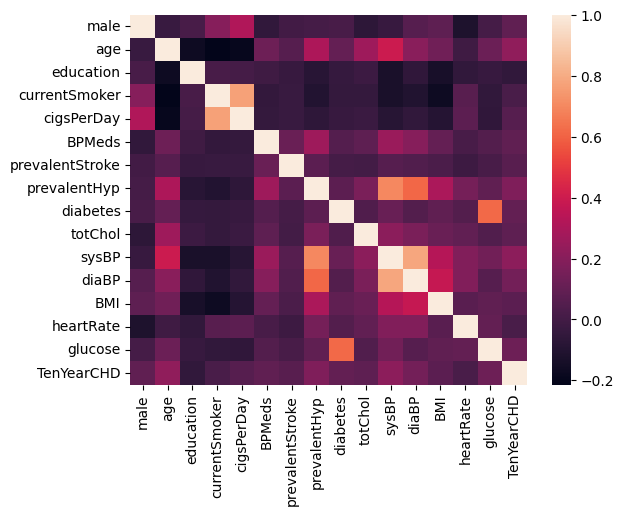
Note: Brighter colors indicate higher correlation while darker colors lower correlations. Therefore, education was excluded from the analysis.

df = df.drop(['education'], axis=1)
# Dropping all rows with missing data
df = df.dropna()
df.isna().sum() # Output is not displayed.
print(df.columns.to_list())

The variable list is:
['male', 'age', 'currentSmoker', 'cigsPerDay', 'BPMeds', 'prevalentStroke', 'prevalentHyp', 'diabetes', 'totChol', 'sysBP', 'diaBP', 'BMI', 'heartRate', 'glucose', 'TenYearCHD']

Step 2: Identify the features (i.e., variables) with the most importance for the outcome variable Heart Disease

Import sckit-learn libraries.

from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2

Note: independent variables (features) in Capital X while dependent (target) variable is small y.

X = df.iloc[:,0:14] # independent variables
y = df.iloc[:,-1]  # target column - 10 year CHD risk

One way of reducing the number of variables to apply SelectKBest class to extract top 10 best features.

bestfeatures = SelectKBest(score_func=chi2, k=10)
fit = bestfeatures.fit(X,y)
dfscores = pd.DataFrame(fit.scores_)
dfcolumns = pd.DataFrame(X.columns)

Combine the above two data frames for better visualization.

featureScores = pd.concat([dfcolumns, dfscores],axis=1) 

featureScores.columns = ['Specs','Score'] # naming the dataframe columns
print(featureScores.nlargest(11,'Score'))  # print 10 best features

Table 1. 10 best correlated variables

	Specs	Score
9	sysBP	667.11
13	glucose	402.41
1	age	297.975
8	totChol	252.959
3	cigsPerDay	185.115
10	diaBP	142.92
6	prevalentHyp	82.3422
7	diabetes	31.7113
4	BPMeds	26.1166
0	male	19.1786
11	BMI	17.1082
5	prevalentStroke	8.48098
12	heartRate	3.63548
2	currentSmoker	0.904429

Step 3. Visualize the selection

plt.figure(figsize=(20,5))
sns.barplot(x='Specs', y='Score', data=featureScores, palette = "GnBu_d")
plt.box(False)
plt.title('Feature importance', fontsize=16)
plt.xlabel('\n Features', fontsize=14)
plt.ylabel('Importance \n', fontsize=14)
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)
plt.show()

Figure 3. Comparison of features in the order of importance

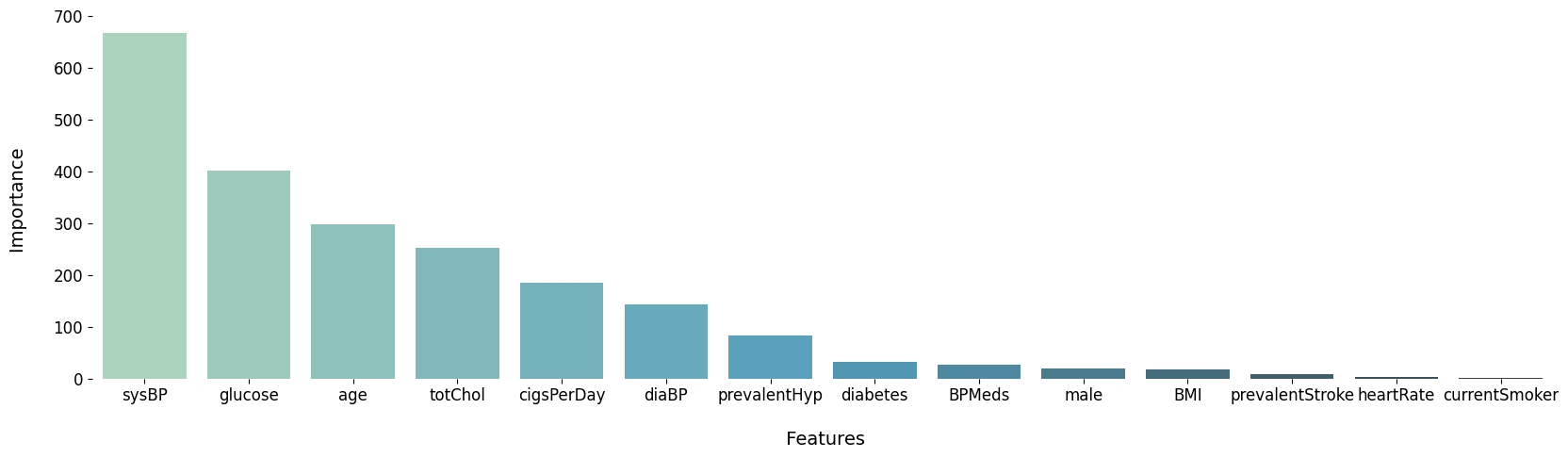
Step 4. Create new dataframe with selected features


df = df[['sysBP', 'glucose','age','totChol','cigsPerDay','diaBP','prevalentHyp','diabetes',
  'BPMeds','male','TenYearCHD']]
df.head()

Table 2. New dataset

id	sysBP	glucose	age	totChol	cigsPerDay	diaBP	BPMeds	male
106	77	39	195	0	70	0	1	0
121	76	46	250	0	81	0	0	0
127.5	70	48	245	20	80	0	1	0
150	103	61	225	30	95	1	0	1
130	85	46	285	23	84	0	0	0

Step 5. Check correlation again


df_corr = df.corr()
sns.heatmap(df_corr)
plt.show()

Figure 5. Heatmap of selected features

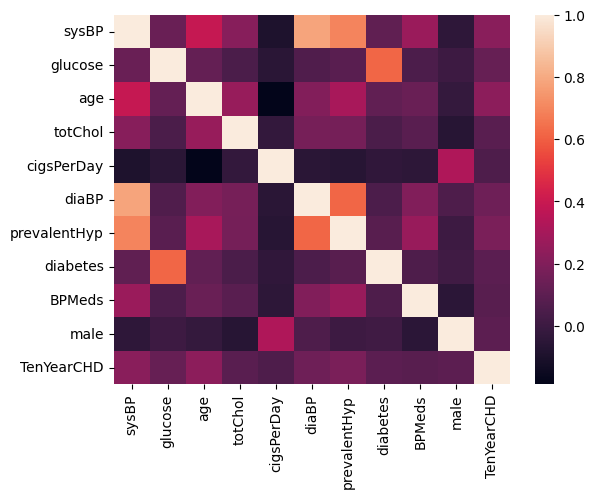
Step 6. Checking for outliers

df.describe() # Output is not shown.
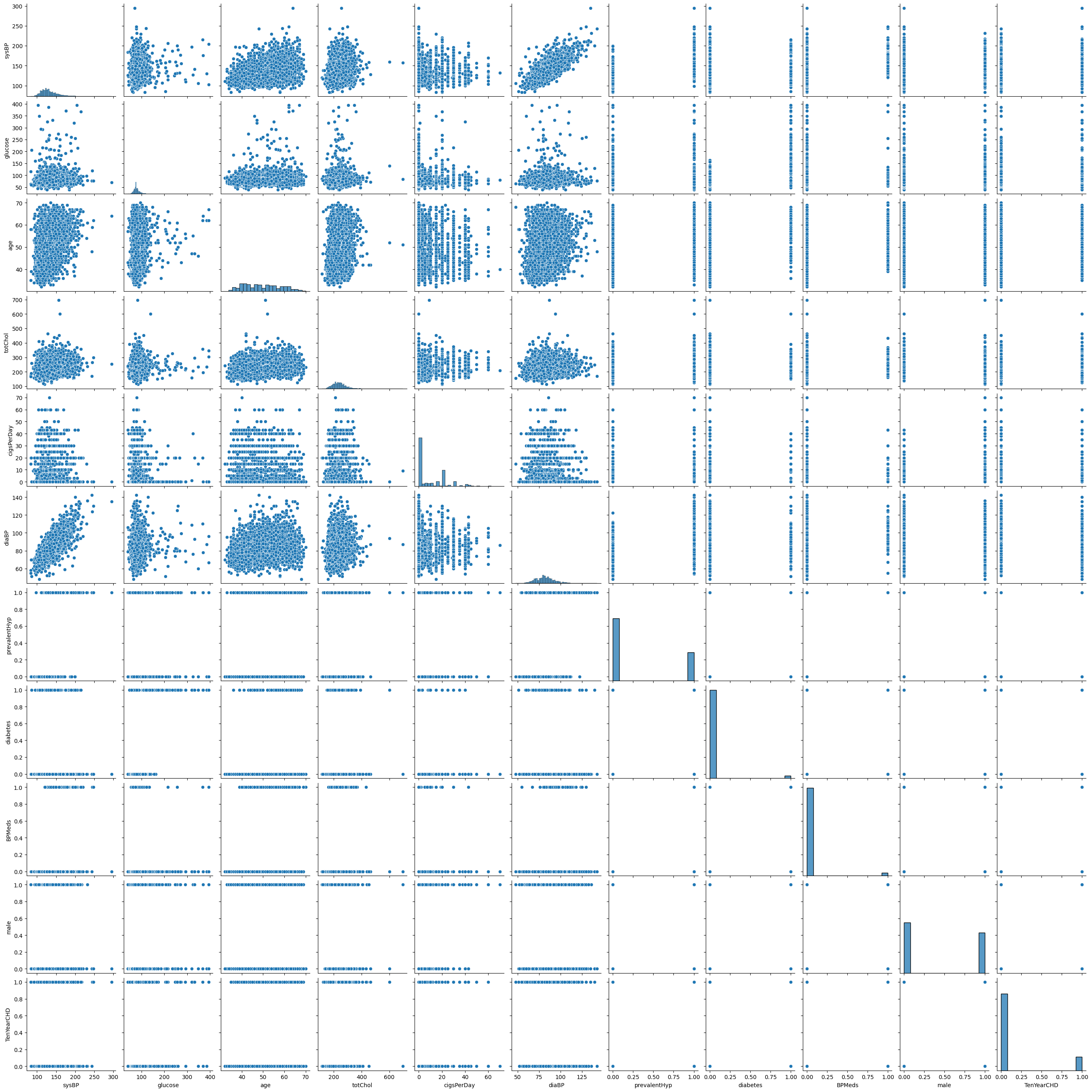
sns.pairplot(df)
plt.show()

Figure 6. Outliers

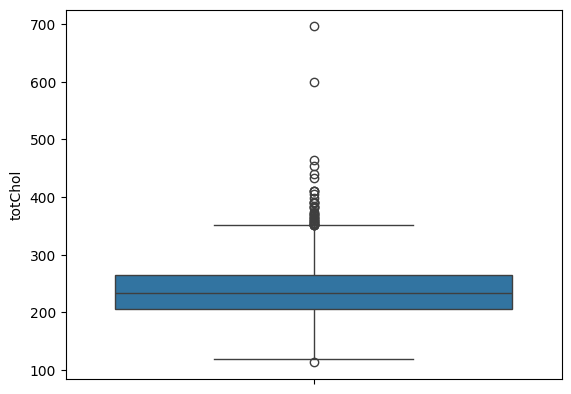
Zooming into cholesterol outliers

sns.boxplot(df.totChol)
outliers = df[(df['totChol'] > 500)]
outliers
plt.show()

Table 3. Two cases of total cholesterol outliers

	sysBP	glucose	age	totChol	cigsPerDay	diaBP	prevalentHyp	diabetes	BPMeds	male	TenYearCHD
1111	159.5	140	52	600	0	94	1	1	0	0	1
3160	157	84	51	696	9	87	1	0	0	1	0

Figure 7. Outliers - Cholesterol

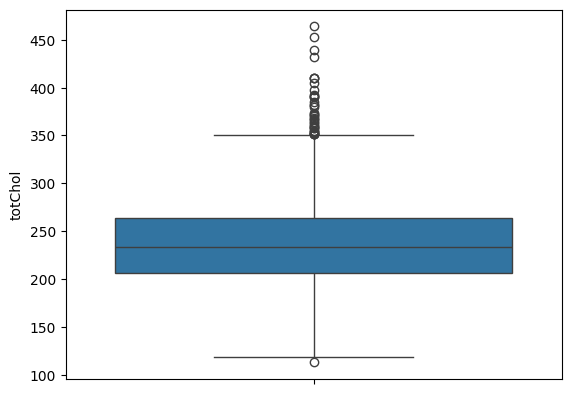
Drop 2 outliers in cholesterol

df = df.drop(df[df.totChol > 599].index)
sns.boxplot(df.totChol)
plt.show()

Figure 8. Outliers Dropped - Cholesterol

Step 7. Preprocessing

In machine learning, the target variable is usually a binary, meaning the value is either 1 (event occurred) or 0 (event not occurred). However, the X features (independent variables or predictors) can be anything (e.g., continous, discrete ordinal, discrete categorical). To be a fair comparison, the units of measurement of X must be compararable to that of y, raning between 0 and 1 [inclusive]. This process is called 'Scale'. It is similar to the standardization (x divided by its standard deviation) where the range of most standardized x can be between - 2 and + 2 (excluding outliers, otherwise the numbers can be huge).

There're several ways of scale: StandardScaler, MinMaxScaler, MaxAbsScaler (according to scikit-learn). These scalers assume the underlying linear relationship between X and y, but I think they can be flexible to adopt non-linear relationship (e.g., quadratic, polynormial, exponentional, logarithmic, or power law, etc.), so that the prediction can be more accurate.

Import scale library.


from sklearn.preprocessing import MinMaxScaler
# Copy the dataset
df_clean = df
# Scale using MiniMaxScaler. This scaler does not change values
# of binary variables when the range is set as (0, 1)
scaler = MinMaxScaler(feature_range=(0,1))

Compare these two datasets.


df_scaled = pd.DataFrame(scaler.fit_transform(df_clean), columns=df_clean.columns)
df_scaled.describe()
df.describe()

Table 4. New dataset - scaled

sysBP	glucose	age	totChol	cigsPerDay	diaBP	prevalentHyp	male	TenYearCHD
0.106383	0.10452	0.184211	0.233618	0	0.232804	0	1	0
0.177305	0.101695	0.368421	0.390313	0	0.349206	0	0	0
0.208038	0.0847458	0.421053	0.376068	0.285714	0.338624	0	1	0
0.314421	0.177966	0.763158	0.319088	0.428571	0.497354	1	0	1
0.219858	0.127119	0.368421	0.490028	0.328571	0.380952	0	0	0

Table 5. Scaled dataset summary

	sysBP	glucose	age	totChol	cigsPerDay	diaBP	prevalentHyp	diabetes	BPMeds	male	TenYearCHD
count	3749	3749	3749	3749	3749	3749	3749	3749	3749	3749	3749
mean	0.231	0.118	0.462	0.352	0.129	0.37	0.312	0.027	0.03	0.445	0.152
std	0.104	0.067	0.226	0.124	0.17	0.126	0.463	0.162	0.172	0.497	0.359
min	0	0	0	0	0	0	0	0	0	0	0
25%	0.158	0.088	0.263	0.265	0	0.286	0	0	0	0	0
50%	0.21	0.107	0.447	0.345	0	0.36	0	0	0	0	0
75%	0.284	0.133	0.632	0.43	0.286	0.444	1	0	0	1	0
max	1	1	1	1	1	1	1	1	1	1	1

Table 6. Original dataset (not scaled)

	sysBP	glucose	age	totChol	cigsPerDay	diaBP	prevalentHyp	diabetes	BPMeds	male	TenYearCHD
count	3749	3749	3749	3749	3749	3749	3749	3749	3749	3749	3749
mean	132.355	81.864	49.572	236.709	9.011	82.935	0.312	0.027	0.03	0.445	0.152
std	22.044	23.87	8.572	43.587	11.927	11.934	0.463	0.162	0.172	0.497	0.359
min	83.5	40	32	113	0	48	0	0	0	0	0
25%	117	71	42	206	0	75	0	0	0	0	0
50%	128	78	49	234	0	82	0	0	0	0	0
75%	143.5	87	56	264	20	90	1	0	0	1	0
max	295	394	70	464	70	142.5	1	1	1	1	1

Continue to Chapter 4. FHS Test, Split, Train

Fallacy of Symptom-Based Inference (Diagnosis) and Prediction (Prognosis)

Table of Contents